[next] [prev] [prev-tail] [tail] [up]

4.2 Matrixformulierung der Quantenmechanik

Es sei Yn der Entwicklungskoeffizient und fn(x) das Basissystem.

sum Y(x) = Yn .fn(x), ^Afn = anfn n

an sei dann der Eigenwert von Â, wobei  beliebig sei.

Y(x) <==> Y1, Y2, Y3, ...

Der Operator ^ B wirke nun auf die Wellenfunktion Y(x):

sum oo ^BY(x) = P(x) = ym .^Bfm(x) m=1

Für P(x) sei nun folgende Entwicklung gegeben:

sum P(x) = fkfk(x)

Wir hängen nun die fk mit den ym zusammen? Dazu bilden wir das Skalarprodukt (fn,P):

sum sum fkfk(x) = ym ^Bfm(x) k m

sum sum ( ^ ) fm fkfk(x) = m ym fm,Bfm(x) k

Dadurch Fallen links alle Glieder bis auch das mit m = k weg:

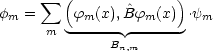
sum ( ) fm = fm(x),B^fm(x) .ym m ------ ------ Bn,m

Bm,n sind die Matrixelemente der Operator B^ bezüglich der Basis fm(x).

sum fn = Bnmym m

In Matrixdarstellung gilt nun:

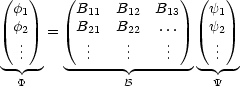
( ) ( ) ( ) f1 B11 B12 B13 y1 f2. = B2.1 B2.2 .... y2. .. .. .. .. .. -P - -------B------- - Y-

Wobei die Regeln für die Multiplikation der Matrix B mit dem Spaltenvektor Y gelten. Eine Matrix wird adjungiert durch:

B '--> B† mit (B †)m,n = B* n,m

Wenn man einen Vektor adjungiert, so schreibt man ihn als Zeilenvektor:

Y † '--> (Y* ,Y*,...) 1 2

Bei Adjungieren eines Produkts gilt:

(AB)† = B†A†

Speziell gilt:

(BY)† = Y†B†

Wir adjungieren die obige Gleichung in Matrixdarstellung:

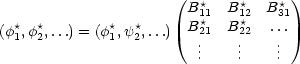
( ) B*11 B*12 B*31 (f*,f*,...) = (f*,y*,...) B*21 B*22 ... 1 2 1 2 .. .. .. . . .

Wir betrachten das Eigenwertproblem eines Operators ^B:

B^Y = bY

In Matrixform ist dieses Problem äquivalent (Matrixeigenwertproblem):

BY = bY

[next] [prev] [prev-tail] [front] [up]