4.3 Dirac’sche Schreibweise

Die Vektoren (x) (Ortswellenfunktion), (p) (Impulswellenfunktion), _m (Spaltenvektor) sid nun Darstellungen eines abstrakten Vektors . ^*, (p)^*, ^* nennen wir nun Bra-Vektor <|. Das Skalarprodukt besitzt folgende Darstellung:

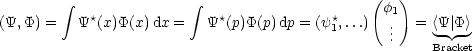
Ein Operator besitzt folgende Darstellung:

Die statischen Zustände des harmonischen Oszillators sind:

Kurz bezeichnet man diese mit |n>. Für dessen Ortsdarstellung gilt:

X sei die Ortseigenfunktion zum Eigenwert x und |n> der Zustand des Oszillators. In Impulsdarstellung gilt analog:

Des weiteren soll die Matrixdarstellung angeführt werden:

Wir stellen Skalarprodukte dar als:

Erwartungswerte berechnen sich dann nach folgender Notation:

Wir geben die Matrixelemente von  bezüglich der Basis |m> an als:

Die Dirac’sche Schreibweise hat den Vorteil, daß man bestimmte Operatoren gut darstellen kann. Wir betrachten = |g><g| mit |g> = g|g>, wobei g> der Eigenvektor und g der zugehörige Eigenwert darstellt.

Wir erhalten somit einen Vektor parallel zu |g>. Ein Operator mit solchen Eigenschaften nennt man Projektionsoperator auf den Vektor |g>.

Es handelt sich hierbei um die Zerlegung des -Operators (Vollständigkeit). Dazu machen wir ein Beispiel:

_n sei hermitesch und es gelte (_m,_n) = _mn. Wir bestimmen die C_m:

Ein Einsoperator kann überall eingeschoben werden:

Gegeben sei (x) (|>) und gefragt sei, wie groß die Wahrscheinlichkeit bei einer Messung der Größe den Eigenwert g_n zu finden.

Also ist |g_n><g_n| der Wahrscheinlichkeitsoperator und <|g_n><g_n|> der Erwartungswert des Wahrscheinlichkeitsoperators.