4.5 Harmonischer Oszillator in algebraischer Behandlung

[next] [prev] [prev-tail] [tail] [up]

4.5 Harmonischer Oszillator in algebraischer Behandlung

Wir erinnern uns an die klassische Physik:

2 2 H = -p- + mw--x2 mit {p,x}= 1 2m 2

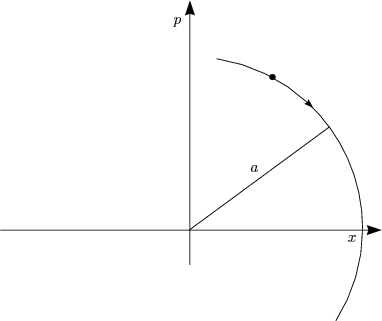
Anstelle vom reellen x und p verwenden wir die komplexe Amplitude a.

x <--> Re(a), p <--> Im(a)

Wir definieren a:

mwx-+-ip a = V~ 2mwh

Es handelt sich um eine dimensionslose komplexe Amplitude. Das wird an dieser Stelle eingeschmuggelt!

^a*= mw V~ x----ip 2mwh

{a,a*}= +ih

In der Quantenmechanik erhalten wir hieraus dann:

† [^a,^a ] = 1

Die freie Bewegung des harmonischen Oszillators läßt sich beschreiben als:

a(t) = |a0| exp(- iwt)

Nun zur Quantentheorie:

^p2 mw2 H^ = ---+ ----^x2 mit [^p,^x] = -ih 2m 2

^a = mw V~ ^x-+i^p, ^a† = mw V~ ^x--i^p 2mhw 2mhw

Durch Einsetzen von â und â^† in den Hamilton-Operator erhalten wir:

( ) H^= 1hw ^a†^a +^a^a† 2

[^a,^a†] = 1, ^a^a†- ^a†^a = 1

Also gilt:

( ) ^ † 1 H = hw ^a ^a + 2

Wir erinnern uns:

( 1) En = hw n + - f¨ur n = 0, 1, 2, ... 2

Wir untersuchen den Operator Â = â^†â = Â^† näher:

^a†^a| a> = a| a > mit a (- R

Wir wollen zeigen, daß > 0:

† <a| ^a- ^a| a> = a<a| a > <b| |b>

Da <|>> 0 und auch <|>> 0 ist, gilt > 0.

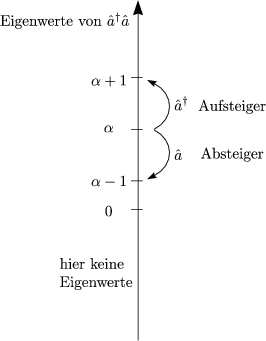
Angenommen, es existieren |> Eigenzustände von Â, dann sind:

^a†|a> = const.|a+ 1> } { a + 1 sind Eigenzust¨ande von A^mit Eigenwert ^a|a> = const.|a -1> a - 1

†(† ) † a^ a^^a|a> = a^a |a>

^a†(^a†^a) = ^a†(^a^a† -1)

(^a†a)(^a†| a>)- ^a†| a > = a^a†| a > = (a+ 1)(^a†|a>)

( † )† † †† ^a a = ^a (^a)

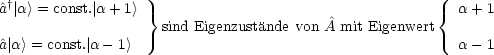
Betrachten wir weiterhin:

^aN|a> = |b> und <b|b> > 0

Für N = 0 gilt nach Voraussetzung <|> = <|> = 1. Für N = 1 erhalten wir:

† <a|^a-^a| a >= a<a|a>= a > 0 a|a> 1

Für N = 2 folgt:

<a|^a† ^a†a^ ^a| a> = <a |(^a†^a)(^a†^a)- (^a†^a)| a> = <a|a2| a = a(a - 1) > 0 ^a^a†- 1

<|>> 0 N erfordert, daß eine natürliche Zahl (einschließlich der Null ist), also gilt: = 0, 1, 2, ....

Grundzustand: |0<, â|0> = 0, <0|0> = 1
|1> = const. ^.â^†|0>
|n> = ⁿ|0> für n = 0, 1, 2, ...

|-†----- V~ ----------| -^a-| n>-=--n-+-1| n-+-1>|

|------ V~ -------| -^a| n-> =-n-|n---1>|

Man kann mit den â^†, â alles ausrechnen, was man mit den Wellenfunktionen ausrechnen kann. Wir berechnen das Matrixelement des Ortsoperators:

V~ ----- ^x = --h- (^a+ ^a†) 2mw

V~ --h--( ) p^= i ---- ^a†- ^a 2mw

V~ ---- V~ ----- V~ ---- h † h ( † ) h [ V~ - V~ ---- ] <m |^x| n> = 2mw-<m|^a+ ^a | n > = 2mw- <m |^a|n>+ <m|^a | n> = 2mw- <m| n |n - 1> + <m | n + 1| n + 1> = V~ ---- V~ ----- = -h--[ V~ n-.dm,n-1 + n+ 1dm,n+1]= Xm,n 2mw

(4.1)

Wir wollen die Ortswellenfunktion des Grundzustandes

₀(x) = exp

bestimmen. Wir starten von der Gleichung, welche den Grundzustand bestimmt:

^a| 0> = 0

mw^x|0>+ i^p|0> = 0

Y0(x) = <x|0>, ^x| x> = x| x>

Wir projizieren diese Gleichung auf den Ortseigenzustand:

mw <x| ^x|0>+ i<x|^p| 0> = 0

Dann gilt mit <x|0> = ₀(x) und <p|0> = ₀(p):

mx<x|0> + i dx'<x| |x'><x'|0>
mx<x|0> + i dp<x| |p><p|0>
|p> ist ein Impuls-Eigenzustand und <x|p> die Ortswellenfunktion des Impuls-Eigenzustandes, also exp mit k = . Es handelt sich um eine Fourier-Transformation:
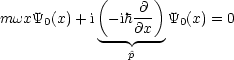
$( ) -@- mwxY0(x) + i -ih@x Y0(x) = 0 ---p^---$

$mw Y'0(x) = --h- x.Y0(x)$
Durch Lösen dieser Differentialgleichung folgt:
$[ 2( )] Y0(x) = const..exp - x- mw- mit c-2 = mw- 2 h h$

$( )n Y (x) = mw^x- h @-- Y (x) m @x 0$

[next] [prev] [prev-tail] [front] [up]