Wir erinnern uns an die Schrödinger-Gleichung:
= (q1,...,qN,t) ist Wellenfunktion, die abhängig ist von N Freiheitsgraden und
der Zeit t. H ist der Hamilton-Operator, der auch von diesen allgemeinen
Koordinaten (und außerdem Impulsen) abhängt:
Eine wichtige Randbedingung für die Funktion ist:
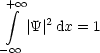
Sie muß also quadratintegrabel sein. Kommen wir nun zum Erwartungswert des Operators O:
Es handelt sich dabei um den Wert, der im Experiment gemessen werden kann. Eine individuelle Messung ist ein Eigenwert.