Unser Ziel ist es nun, die stationären Lösungen der zeitunabhängigen eindimensionalen Schrödingergleichung zu erhalten. Eine stationäre Lösung läßt sich schreiben als:
Durch Einsetzen in die Schrödingergleichung resultiert:
Zur Lösung dieser Gleichung machen wir nun folgenden Ansatz:
S und A seien gerade Funktionen von ![]() . Man erhält dann:
. Man erhält dann:
Gleichung (4) wird gelöst durch:
Aus (4) und (5) erhalten wir dann schließlich:
![|-------------------------------------------|
| [ ( '')2 '''] |
|S'2 = 2m(E - V )+ h2 3 S-' - 1S-' (6)|
---------------------4--S-------2S-----------](th18x.gif)
Interessant ist nun, daß wir bisher eine exakte Rechnung durchgeführt haben. An dieser Stelle werden wir jetzt die WKB-Näherung verwenden:
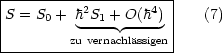
Auch Gleichung (6) resultiert dann mit dieser Näherung:
Wir unterscheiden zwei Fälle:
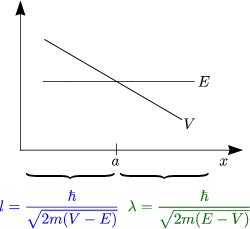
Wir definieren eine „Wellenlänge“ (![]() :=
:= ![]() ):
):
Es gilt näherungsweise:
Für die allgemeine Lösung folgt dann:
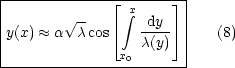
![]() und x0 seien Konstanten.
und x0 seien Konstanten.
Es wird eine sogenannte Eindringtiefe („Skin-depth“ l := ![]() ) definiert:
) definiert:
Die allgemeine Lösung lautet hier nun:
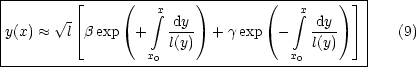
Ein Kriterium für die Exaktheit der Näherung ist:
Oder auch:
Die Näherung ist sicherlich nicht erfüllt für die Umkehrpunkte xn .V (xn) = E. Das Fazit besteht nun darin, die Anschlußbedingungen einzuführen:
| x « a | x » a | ||
y1 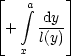 (13) (13) | | y1 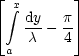 (15) (15) | |
y2 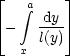 (14) (14) | | y2 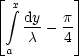 (16) (16) | |
Die Voraussetzungen dafür, daß dies stimmt, sind:
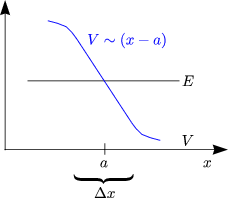

Nicht erlaubt ist beispielsweise so etwas:
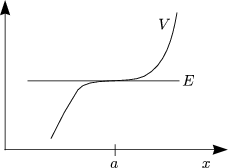
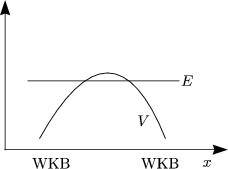
ABER VORSICHT! Wenn im Bereich x « a gilt, daß ![]() exakt
exakt ![]() Ay1 mit A
Ay1 mit A![]() 0, kann
man auch daß
0, kann
man auch daß ![]() exakt
exakt ![]() Ay1 + By2 mit beliebigem B schreiben. Also ist im Bereich
x » a die Lösung unbestimmt:
Ay1 + By2 mit beliebigem B schreiben. Also ist im Bereich
x » a die Lösung unbestimmt:
Nur wenn im Bereich x « a sicher ist, daß ![]() exakt = By2 (A = 0), findet man im
Bereich x » a sicher:
exakt = By2 (A = 0), findet man im
Bereich x » a sicher:
Für x « a gelte ![]() exakt = By2 und für x » a By2.
exakt = By2 und für x » a By2.