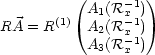mit dem Eigenwert s(s + 1) = 
von 
2.
Für die Eigenvektoren von 
2 und Sz folgt:
Angenommen, wir haben einen Spinvektor mit dem Eigenwert s(s + 1) = von 2.
Für die Eigenvektoren von 2 und Sz folgt:
Wir können 
mit den Pauli-Matrizen darstellen:
Dann können wir die Eigenvektoren auch darstellen als Spinoren
Spinoren sind keine Zweiervektoren!
Betrachten wir eine Drehung Rû(
):
![[ ] ( ) ( )
R(u1^/2)(f) = exp -ifs-.^u = cos f- 12- sin f- is .^u mit R(2p) = -1
2 2 2](th294x.gif){kind=small}
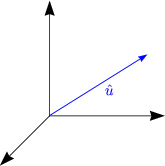
Die letzte Beziehung ergibt sich durch Betrachtung der Taylor-Entwicklung der
Exponentialfunktion. Betrachten wir nun ein Teilchen mit Spin 
. Dieses habe die
Bahnvariablen rk und pk und es gelte [rk,pl] = i
kl. Für die Spinvariablen
gilt:
![[r ,S ] = 0 = [p ,S],| S |2 = 31, [S ,S ] = ie S
k l k l 4 k l klm m](th296x.gif){kind=small}
Der Zustandsraum ist das Tensorprodukt E = EOrt 
ESpin. Wir betrachten die
Darstellung mit 
und diagonalem Sz:
Der Gesamtdrehimpuls 
setzt sich zusammen aus Bahndrehimpuls 
und Spin
:
Wir schreiben nun die Wellenfunktion in Zweikomponentenform:
Wir wollen das als Spinorfeld bezeichnen. Machen wir eine Drehung, so wird das Spinorfeld auch gedreht. Erstens wird die Position des Feldes gedreht, zweitens ändern sich die Komponenten.
Zum Vergleich notieren wir uns die Drehung eines Skalarfeldes und eines Vektorfeldes:
